Rumus Trigonometri – Pengantar
Dalam trigonometri, Sinus. Cosinus. Tangent, Cosecan, Secan, dan Cotangent bisa digunakan bersama-sama baik dengan penjumlahan atau pengurangan maupun perkalian. Rumus-rumus penjumlahan, pengurangan, atau perkalian dalam trigonometri dapat diturunkan dari rumus jumlah dua sudut atau selisih dua sudut.
Rumus Trigonometri untuk Jumlah Dua Sudut dan Selisih Sudut
Rumus Trigonometri untuk Sudut Rangkap
Pada rumus sudut rangkap, merupakan modifikasi dari penjumlahan dua sudut dengan 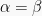 , sehingga rumusnya menjadi sebagi berikut:
, sehingga rumusnya menjadi sebagi berikut:
Subtitusikan 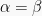 pada persamaan diatas, sehingga menjadi:
pada persamaan diatas, sehingga menjadi:
Karena 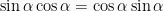 , maka didapat:
, maka didapat:
Sifat I: 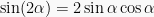 .
.
Subtitusikan 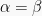 pada persamaan diatas, sehingga menjadi:
pada persamaan diatas, sehingga menjadi:
Karena 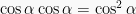 dan
dan  , maka didapat:
, maka didapat:
Sifat II:  .
.
Karena hasil pada cos sudut rangkap (II) merupakan selisih kuadrat, maka bentuk ini bisa disubtitusi dengan identitas trigonometri:
Subtitusikan 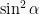 pada persamaan rumus sudut rangkap dari cos (II) menjadi:
pada persamaan rumus sudut rangkap dari cos (II) menjadi:
Buka kurung pada persamaan menjadi:
Jumlah kan kuadrat dari kedua cos akan didapat:
Sifat III: 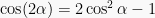 .
.
Subtitusikan  pada persamaan rumus sudut rangkap dari cos (II) menjadi:
pada persamaan rumus sudut rangkap dari cos (II) menjadi:
Buka kurung pada persamaan menjadi:
Jumlah kan kuadrat dari kedua cos didapat:
Sifat IV: 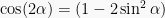 .
.
Rumus Trigonometri untuk Perkalian Sinus dan Cosinus
Rumus perkalian dari Sinus dan Cosinus diperoleh dari menjumlahkan dan mengurangi rumus dari sudut rangkap.
Rumus Pertama:
Jumlahkan  dengan
dengan 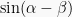 :
:

Dari perhitungan hasil diatas diperoleh:
Rumus Kedua:
Kurangkan  dengan
dengan 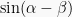 :
:

Dari perhitungan hasil diatas, diperoleh:
Rumus Ketiga:
Jumlahkan  dengan
dengan 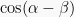 :
:

Dari perhitungan hasil diatas diperoleh:
Rumus Keempat:
Kurangkan dengan  dengan
dengan 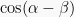 :
:

Dari perhitungan hasil diatas diperoleh:
Rumus Trigonometri untuk Penjumlahan dan Pengurangan Sinus dan Cosinus
Rumus trigonometri untuk penjumlahan dan pengurangan merupakan modifikasi dari bentuk perkalian Sinus dan Cosinus.
Pada modifikasi ini, kita cukup mensubtitusi 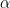 menjadi
menjadi 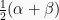 dan
dan 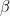 menjadi
menjadi 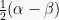 , sehingga diperoleh:
, sehingga diperoleh:
Rumus Trigonometri Pada Segitiga
Aturan Sinus
Setiap segitiga, selalu memiliki tiga sudut dan setiap sudut selalu menghadap pada satu sisi. Dari masing-masing sudut dan sisi yang berhadapan, terdapat perbandingan yang selalu sebanding, yaitu:
Aturan Sinus ini dapat digunakan dalam perhitungan jika paling sedikit diketahui 2 sisi 1 sudut atau 1 sisi 2 sudut.
Aturan Cosinus
Rumus perbandingan sudut dengan sisi pada segitiga, selain menggunakan Sinu, juga terdapat rumus Cosinus, yaitu:
Rumus diatas digunakan untuk menentukan panjang sisi jika diketahui 2 sisi dan 1 sudut yang diapit kedua sisi tersebut.
Sedangkan untuk menentukan besar sudut jika diketahui 3 sisi segitiga, dapat menggunakan aturan ini juga, dengan mengubah bentuk di atas, misalnya:
Contoh Soal
Sederhanakah bentuk persamaan berikut 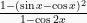 !
!
Jawab:
Penjabaran dari bentuk 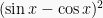 adalah
adalah 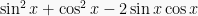 , dimana
, dimana  sesuai identitas trigonometri, sehingga:
sesuai identitas trigonometri, sehingga:
Untuk bentuk  , dengan menggunakan rumus sudut rangkap, diperoleh bentuk
, dengan menggunakan rumus sudut rangkap, diperoleh bentuk 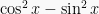 ,
,  , atau
, atau 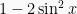 . Untuk penyelesaian persamaan ini, kita gunakan bentuk
. Untuk penyelesaian persamaan ini, kita gunakan bentuk 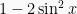 .
.
Sehingga persamaan menjadi:
Ketika tanda kurung dihilangkan, menjadi:
Bagi pembilang dan penyebut dengan  , dan diperoleh bentuk:
, dan diperoleh bentuk: