Gelombang Stasioner Fisika: Contoh dan Latihan Soal Lengkap Pembahasannya
diperlukan koneksi internet untuk dapat melihat gambar soal dan jawaban!!
Nomor 1
Diberikan sebuah persamaan gelombang Y = 0,02 sin (10πt − 2πx) dengan t dalam sekon, Y dan x dalam meter.
Tentukan:
a. amplitudo gelombang
b. frekuensi sudut gelombang
c. tetapan gelombang
d. cepat rambat gelombang
e. frekuensi gelombang
f. periode gelombang
g. panjang gelombang
h. arah rambat gelombang
i. simpangan gelombang saat t = 1 sekon dan x = 1 m
j. persamaan kecepatan gelombang
k. kecepatan maksimum gelombang
l. persamaan percepatan gelombang
m. nilai mutlak percepatan maksimum
n. sudut fase saat t = 0,1 sekon pada x = 1/3 m
o. fase saat t = 0,1 sekon pada x = 1/3 m
Pembahasan :
Bentuk persamaan umum gelombang:
Y = A sin (ωt – kx)
dengan A amplitudo gelombang, ω = 2πf dan k = 2π/λ dengan demikian :
a. A = 0,02 m
b. ω = 10π rad/s
c. k = 2π
d. v = ω/k = 10π/2π = 5 m/s
e. f = ω/2π = 10π/2π = 5 Hz
f. T = 1/f = 1/ 5 = 0, 2 sekon
g. λ = 2π/k = 2π/2π = 1 m
h. ke arah sumbu x positif
i. Y = 0,02 sin(10 π- 2π) = 0,02 sin(8π) = 0 m
j. v = ω A cos(ωt−kx) = 10π(0,02) cos(10πt−2πx) m/s
k. vmaks = ωA = 10π(0,02) m/s
l. a = −ω2y = −(10π)2 (0,02) sin(10πt − 2πx) m/s2
m. amaks = |−ω2A| = |−(10π)2 (0,02)| m/s2
n. sudut fase θ = (10.π.0,1−2π.(1/3) = 1/3 π = 60o
o. fase φ = 60o/360o = 1/6
Nomor 2
Suatu gelombang permukaan air yang frekuensinya 500 Hz merambat dengan kecepatan 350 m/s. tentukan jarak antara dua titik yang berbeda sudut fase 60°!
(Sumber : Soal SPMB)
Pembahasan :
Lebih dahulu tentukan besarnya panjang gelombang dimana
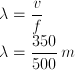
Beda fase gelombang antara dua titik yang jaraknya diketahui adalah

Nomor 3
Seutas tali salah satu ujungnya digerakkan naik turun sedangkan ujung lainnya terikat. Persamaan gelombang tali adalah y = 8 sin (0,1π) x cos π (100t – 12) dengan y dan x dalam cm dan t dalam satuan sekon. Tentukan:
a. panjang gelombang
b. frekuensi gelombang
c. panjang tali
(Sumber : Soal Ebtanas)
Pembahasan :
Pola dari gelombang stasioner diatas adalah

a. menentukan panjang gelombang

b. menentukan frekuensi gelombang

c. menentukan panjang tali

Nomor 4
Diberikan grafik dari suatu gelombang berjalan seperti gambar di bawah!

Jika jarak P ke Q ditempuh dalam waktu 5 sekon, tentukan persamaan dari gelombang di atas! (Tipikal Soal UN)
Pembahasan :
Bentuk umum persamaan gelombang adalah

atau

atau
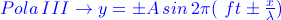
dengan perjanjian tanda sebagai berikut :
Tanda Amplitudo (+) jika gerakan pertama ke arah atas
Tanda Amplitudo (-) jika gerakan pertama ke arah bawah
Tanda dalam kurung (+) jika gelombang merambat ke arah sumbu X negatif / ke kiri
Tanda dalam kurung (-) jika gelombang merambat ke arah sumbu X positif / ke kanan
ambil data dari soal panjang gelombang (λ) = 2 meter, dan periode (T) = 5/2 sekon atau frekuensi (f) = 2/5 Hz, masukkan data ke pola misal pola ke 2 yang dipakai didapat
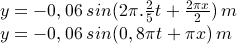
Nomor 5
Seutas kawat bergetar menurut persamaan :
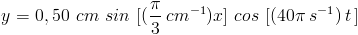
Jarak perut ketiga dari titik x = 0 adalah…..
A. 10 cm
B. 7,5 cm
C. 6,0 cm
D. 5,0 cm
E. 2,5 cm
Sumber Soal : Marthen Kanginan 3A Gejala Gelombang
Pembahasan :
Pola diatas adalah pola untuk persamaan gelombang stasioner ujung tetap atau ujung terikat. Untuk mencari jarak perut atau simpul dari ujung ikatnya, tentukan dulu nilai dari panjang gelombang.
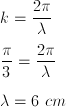
Setelah ketemu panjang gelombang, tinggal masukkan rumus untuk mencari perut ke -3 . Lupa rumusnya,..!?! Atau takut kebalik-balik dengan ujung bebas,..!? Ya sudah tak usah pakai rumus, kita pakai gambar saja seperti di bawah:

Posisi perut ketiga P3 dari ujung tetap A adalah satu seperempat panjang gelombang atau (5/4) λ (Satu gelombang = satu bukit – satu lembah), sehingga nilai X adalah :
X = (5/4) λ = (5/4) x 6 cm = 7,5 cm
Nomor 6
Sebuah gelombang transversal memiliki frekuensi sebesar 0,25 Hz. Jika jarak antara dua buah titik yang berurutan pada gelombang yang memiliki fase sama adalah 0,125 m, tentukan cepat rambat gelombang tersebut, nyatakan dalam satuan cm/s!
Pembahasan
Data dari soal:
f = 0,25 Hz
Jarak dua titik yang berurutan dan sefase:
λ = 0, 125 m
ν = …..
ν = λ f
ν = (0,125)(0,25) = 0,03125 m/s = 3,125 cm/s
Nomor 7
Sebuah gelombang transversal memiliki frekuensi sebesar 0,25 Hz. Jika jarak antara dua buah titik yang berurutan pada gelombang yang memiliki fase berlawanan adalah 0,125 m, tentukan cepat rambat gelombang tersebut, nyatakan dalam satuan cm/s!
Pembahasan
Data dari soal:
f = 0,25 Hz
Jarak dua titik yang berurutan dan berlawanan fase:
1/2λ = 0, 125 m → λ = 2 × 0,125 = 0,25 m
ν = …..
ν = λ f
ν = (0,25)(0,25) = 0,0625 m/s = 6,25 cm/s
Nomor 8
Diberikan sebuah persamaan gelombang:
y = 0,05 cos (10t + 2x) meter
Tentukan :
a) Persamaan kecepatan
b) Persamaan percepatan
Pembahasan
( y)
↓ diturunkan
( ν)
↓ diturunkan
( a)
y = 0,05 cos (10t + 2x) meter
Jika y diturunkan, akan diperoleh v :
ν = − (10)(0,05) sin (10t + 2x)
ν = − 0,5 sin (10t + 2x) m/s
Jika v diturunkan, akan diperoleh a :
a = − (10)(0,5) cos (10t + 2x)
a = − 5 cos (10t + 2x) m/s2
Artikel Terkait materi ini bisa ditengok:
Bank Soal Semester Gelombang Berjalan,
Bank Soal Semester Gelombang Stasioner
Persamaan gelombang stationer ujung bebas
Persamaan gelombang berjalan ujung terikat
Soal No. 9
Persamaan simpangan gelombang berjalan y = 10 sin π(0,5t −2x). Jika x dan y dalam meter serta t dalam sekon maka cepat rambat gelombang adalah….
A. 2,00 m.s−1
B. 0,25 m.s−1
C. 0,10 m.s−1
D. 0,02 m.s−1
E. 0,01 m.s−1
(Soal Gelombang – UN Fisika 2009)
Pembahasan
Menentukan cepat rambat gelombang dari suatu persamaan simpangan gelombang, bisa dengan beberapa cara, diantaranya:
– mencari frekuensi dan panjang gelombang terlebih dahulu, kemudian menggunakan rumus ν = λ f
– mengambil ω dan k dari persamaan gelombang, kemudian memakai rumus ν = ω / k seperti contoh 1 point d.
– mengambil koefisien t dan koefisien x, kemudian menggunakan ν = koefisien t / koefisien x
Kita ambil cara yang ketiga saja:

Soal No. 10
Sebuah gelombang berjalan di permukaan air memenuhi persamaan y = 0,03 sin 2π (60 t − 2x), y dan x dalam meter dan t dalam sekon. Cepat rambat gelombang tersebut adalah….
A. 15 m.s−1
B. 20 m.s−1
C. 30 m.s−1
D. 45 m.s−1
E. 60 m.s−1
(Soal Gelombang – UN Fisika 2011)
Pembahasan
Dengan cara yang sama nomor sebelumnya:

Soal pembahasan tentang gelombang yang lain silahkan dibuka berikut ini.
Soal No. 11
Pada tali yang panjangnya 2 m dan ujungnya terikat pada tiang ditimbulkan gelombang stasioner. Jika terbentuk 5 gelombang penuh, maka letak perut yang ke tiga dihitung dari ujung terikat adalah…
A. 0,10 meter
B. 0,30 meter
C. 0,50 meter
D. 0,60 meter
E. 1,00 meter
(Soal Gelombang Stasioner Ujung Tetap – Ebtanas 1992)
Pembahasan
Terlihat, dalam 2 meter (200 cm) ada 5 gelombang. Jadi untuk 1 gelombangnya, panjangnya adalah
λ = 200 cm/5 = 40 cm.

Perut ketiga, jika dihitung dari ujung ikatnya berjarak 1 gelombang lebih 1/4, atau 5/4 gelombang. Jadi jaraknya adalah:
x = 5/4 × λ
x = 5/4 × 40 cm = 50 cm = 0,5 meter.
Soal No. 12
Seutas tali digetarkan pada salah satu ujungnya sehingga menghasilkan gelombang seperti gambar.

Jika ujung tali digetarkan selama 0,5 s maka panjang gelombang dan cepat rambat gelombang berturut-turut adalah….(Sampel UN 013)
A. 25 cm dan 100 cm/s
B. 25 cm dan 50 cm/s
C. 50 cm dan 25 cm/s
D. 50 cm dan 100 cm/s
E. 125 cm dan 25 cm/s
Pembahasan
Untuk dua buah gelombang = 50 cm
Jadi satu gelombangnya λ = 50 cm / 2 = 25 cm
Cepat rambat:
50 cm / 0,5 s = 100 cm/s
Soal No. 13
Akibat adanya pemantulan, terbentuk gelombang stasioner dengan persamaan:
y = 0,5 sin (0,4 π x) cos π(10t – 4) meter
Dari persamaan di atas, kelajuan gelombang pantulnya adalah …
A. 2 m/s
B. 4 m/s
C. 5 m/s
D. 10 m/s
E. 25 m/s
Jawaban : E
Pembahasan :
persamaan umum gelombang stasioner ujung terikat adalah y = 2A sin kx cos ωt sehingga
nilai k = 0,4 π
nilai ω = 10 π
kelajuan gelombang v = ω/k = 10 π/(0,4 π) = 25 m/s
Soal No. 14
Suatu gelombang stasioner memiliki persamaan y = 40 cos 2π x sin 100π t. x dan y dalam cm dan t dalam sekon. Pernyataan berikut berkaitan dengan gelombang stasioner tersebut.
1) Amplitudo gelombang sumber adalah 40 cm.
2) Frekuensi gelombang sumber 50 Hz.
3) Panjang gelombang sumber adalah 50 cm.
4) Cepat rambat gelombang sumber adalah 250 cm/s.
Pernyataan di atas yang benar adalah ……
a. 1), 2), dan 3)
b. 1) dan 3)
c. 2) dan 4)
d. 4) saja
e. 1), 2), 3), dan 4)
Jawab : C
Pembahasan :
dari persamaan y = 40 cos 2π x sin 100π t dapat diketahui
2A = 40 cm
k = 2π [ k = 2π/λ ]
ω = 100π [ ω = 2πf ]
Ampitudo gelombang sumber A = 40/2 = 20 cm (pernyataan 1 salah)frekuensi f = ω/2π = 100π/2π = 50 Hz (pernyataan 2 benar)Panjang gelombang λ = 2π/k = 2π/2π = 1 cm (pernyataan 3 salah)Cepat rambat gelombang v = ω/k = 100π/2π = 50 cm/s (pernyataan 4 benar)
Soal No. 15
Suatu gelombang stasioner mempunyai persamaan : y = 0,2 cos 5πx sin 10πt (y dan x dalam meter dan t dalam waktu). Jarak antara perut dan simpul yang berturutan pada gelombang ini adalah …
A. 0,1 m
B. 0,2 m
C. 0,4 m
D. 2,5 m
E. 5,0 m
Jawaban : A
Pembahasan :
perhatikan pertanyaannya : jarak antara perut dan simpul yang berurutan.
Dari gambar gelombang, jarak antara perut dan simpul yang berurutan adalah sama dengan seperempat gelombang ( ¼ λ) sehingga kita harus mencari besar panjjang gelombang (λ).
k = 2π/λ
λ = 2π/k = 2π/5π = 0,4 m.
sehingga jarak antara perut dan simpul yang berurutan = ¼ λ = ¼ x 0,4 = 0,1 m
Soal No. 16
Pada tali yang panjangnya 2 m dan ujungnya terikat pada tiang ditimbulkan gelombang stasioner. Jika
terbentuk 5 gelombang penuh, maka letak perut yang ke tiga dihitung dari ujung terikat adalah …
A. 0,10 meter
B. 0,30 meter
C. 0,50 meter
D. 0,60 meter
E. 1,00 meter
Jawaban : C
Pembahasan :
perhatikan gambar gelombang stasioner ujung terikat berikut ini
Dari gambar di atas dapat diketahui bahwa letak perut ke 3 sama dengan 1¼ λ. sehingga langkah pertama harus mencari λ
INGAT!!! λ = panjang 1 gelombang, jika panjang keseluruhan 2 m menghasilkan 5 gelombang, maka satu gelombang = λ = 2/5 = 0,4 m.
sehingga letak perut ke tiga dari ujung terikat = 1¼ λ = 5/4 x 0,4 = 0,5 m.
Soal No. 17
Sebuah gelombang transversal merambat menurut persamaan y = 0,5 sin (8πt – 2πx) m. Tentukanlah:
a) arah gelombang ?
b) Amplitudo gelombang ?
c) simpangan pada x = 0,5 m ketika t = 1 s
d) frekuensi dan periode gelombang ?
e) Panjang gelombang
f) Cepat rambat gelombang
JAWAB :
Diketahui persamaan gelombang y = 0,5 sin (8πt – 2πx) m
maka Amplitudo A = 0,5 m, kecepatan sudut ω = 8π rad/s dan bilangan gelombang k =2π rad/m
a) karena persamaan bertanda negatif maka gelombang bergerak ke arah kanan ( sumbu x +)
b) A = 0,5 m
c) x = 0,5 m dan t = 1
y = 0,5 sin (8π (1) – 2π(0,5))
y = 0,5 sin 7π
y = 0,5 (0)
y = 0
d) ω = 8π
2πf = 8π f = 4 Hz T = 1/f = 1/4 = 0,25 s
e) k = 2π
2π/λ = 2π λ = 1 m

