Gerak Parabola Fisika : Contoh Soal dan Pembahasan, Soal Latihan, Ilustrasi Gambar
diperlukan koneksi internet untuk dapat melihat gambar soal dan jawaban!!
Contoh soal dan pembahasan gerak parabola berikut ini ditampilkan 3 tipe soal dari topik Gerak Parabola yang dibahas di materi kelas XI IPA SMA, kecepatan peluru pada sumbu x sumbu y, jarak yang ditempuh peluru pada waktu tertentu, jarak terjauh, tinggi maksimum yang dicapai peluru dan sudut-sudut elevasi gerak peluru atau gerak projektile:
1) Soal Tipe I Normal Parabolik
Perhatikan gambar berikut ini! Sebuah peluru ditembakkan dengan kelajuan awal 100 m/s dan sudut elevasi 37o . Jika percepatan gravitasi bumi 10 m/s2, sin 37o = 3/5 dan cos 37o = 4/5
Tentukan:
a) Penguraian vektor kecepatan awal terhadap arah horizontal (sumbu X)
b) Penguraian vektor kecepatan awal terhadap arah vertikal (sumbu Y)
c) Kecepatan peluru saat t = 1 sekon
d) Arah kecepatan peluru saat t = 1 sekon terhadap garis mendatar (horisontal)
e) Tinggi peluru saat t = 1 sekon
f) Jarak mendatar peluru saat t = 1 sekon
g) Waktu yang diperlukan peluru untuk mencapai titik tertinggi
h) Kecepatan peluru saat mencapai titik tertinggi
i) Tinggi maksimum yang bisa dicapai peluru ( Ymaks )
j) Waktu yang diperlukan peluru untuk mencapai sasaran (jarak terjauh arah mendatar)
k) Jarak terjauh yang dicapai peluru ( Xmaks )
Pembahasan
a) Penguraian vektor kecepatan awal terhadap arah horizontal (sumbu X)
b) Penguraian vektor kecepatan awal terhadap arah vertikal (sumbu Y)
c) Kecepatan peluru saat t = 1 sekon
Karena gerak parabola terbentuk dari dua buah jenis gerak, yaitu GLBB pada sumbu Y dan GLB pada sumbu X, maka terlebih dahulu harus dicari kecepatan gerak peluru saat 1 sekon untuk masing-masing sumbu.
Pada sumbu X :
Karena jenis geraknya GLB (gerak lurus beraturan) maka kecepatannya selalu konstan , jadi akan sama dengan kecepatan awal untuk sumbu X jadi :
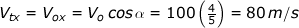
sumbu Y:
Jenis gerakan pada sumbu Y adalah GLBB jadi ingat rumus untuk mencari kecepatan saat t yaitu Vt = Vo - gt dengan Vo disini diganti Vo miliknya Y atau Voy
kecepatan ” saja
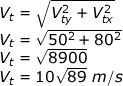
d) Arah kecepatan peluru saat t = 1 sekon terhadap garis mendatar (horisontal)
Arah kecepatan bisa diwakili oleh nilai sinus, cosinus atau tan dari suatu sudut, kalo mau sudutnya tinggal ubah saja jika sudah diketahui nilai sin, cos tan nya. Disini kita pakai nilai tan sudut katakanlah namanya sudut Θ dimana:
Besar sudutnya…, cari pakai kalkulator karena bukan sudut istimewa.
e) Tinggi peluru saat t = 1 sekon
Saat 1 sekon ketinggian peluru namakan saja Y atau h juga boleh,…
f) Jarak mendatar peluru saat t = 1 sekon
Saat 1 sekon jarak mendatar peluru namakan saja X
g) Waktu yang diperlukan peluru untuk mencapai titik tertinggi
Titik tertinggi dicapai peluru saat kecepatan pada sumbu Y adalah NOL. Sehingga:
h) Kecepatan peluru saat mencapai titik tertinggi
Karena saat titik tertinggi Vty = 0, maka tinggal Vtx saja yang ada nilainya sehingga:
Vt = Vtx = Vo cos α = 100(4/5) = 80 m/s
i) Tinggi maksimum yang bisa dicapai peluru
Tinggi maksimum namakan Y maks atau di soal biasanya hmax,..tinggal pilih saja :
j) Waktu yang diperlukan peluru untuk mencapai sasaran (jarak terjauh arah mendatar)
Waktu untuk mencapai jarak mendatar paling jauh adalah dua kali waktu untuk mencapai ketinggian maksimum sehingga hasilnya 2 x 6 = 12 sekon.
k) Jarak terjauh yang dicapai peluru
Cara pertama, dipakai jika sudah diketahui waktunya (12 sekon)
Xmaks = (Vo cos α ) t = 100(4/5)12 = 960 meter
Cara kedua anggap saja belum diketahui waktunya :
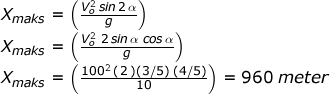
2) Soal Tipe II Setengah Parabolik
Sebuah peluru ditembakkan dari moncong sebuah meriam dengan kelajuan 50 m/s arah mendatar dari atas sebuah bukit, ilustrasi seperti gambar berikut.
Jika percepatan gravitasi bumi adalah 10 m/s2 dan ketinggian bukit 100 m
Tentukan :
a. Waktu yang diperlukan peluru untuk mencapai tanah
b. Jarak mendatar yang dicapai peluru (S)
a) Waktu yang diperlukan peluru untuk mencapai tanah
Tinjau gerakan sumbu Y, yang merupakan gerak jatuh bebas. Sehingga Voy = O dan ketinggian bukit namakan Y (di soal dinamakan h)
Y = 1/2 g t2
100 = (1/2)(10) t2
t = √20 = 2√5 sekon
b) Jarak mendatar yang dicapai peluru (S)
Jarak mendatar gerakan berupa GLB karena sudutnya nol terhadap horizontal langsung saja pakai rumus:
S = V t
S = (50)( 2 √5) = 100 √5 meter
3) Soal Tipe III
Sebuah bola dilontarkan dari atap sebuah gedung yang tingginya adalah h = 10 m dengan kelajuan awal V0 = 10 m/s
Jika percepatan gravitasi bumi adalah 10 ms2 , sudut yang terbentuk antara arah lemparan bola dengan arah horizontal adalah 30o dan gesekan bola dengan udara diabaikan,,
Tentukan :
a) Waktu yang diperlukan bola untuk menyentuh tanah
b) Jarak mendatar yang dicapai bola
Pembahasan
a) Waktu yang diperlukan bola untuk menyentuh tanah ketinggian gedung h atau sama dengan Y disini :
ambil nilai positif sehingga t = 2 sekon
Catatan : Jangan lupa tanda minus pada nilai Y, karena kalau plus berarti 10 meter diatas tempat pelemparan, sementara posisi yang dicari adalah 10 meter dibawah tempat pelemparan.
b) Jarak mendatar yang dicapai bola
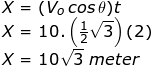
Setelah belajar soal tipe dasar, lanjut dengan soal-soal yang lain atau bisa lanjut ke soal-soal pengayaan,
Soal No. 4
Sebuah peluru ditembakkan dengan kecepatan 60 m/s dan sudut elevasi 30°. Ketinggian maksimum yang dicapai adalah….
A. 30 m
B. 45 m
C. 50 m
D. 90 m
E. 100 m
(Sumber soal UMPTN 1997)
Pembahasan
Data dari soal:
vo = 60 m/s
α = 30°
Ymaks = ……
vo 2 sin2 α
Ymaks = _______________________
2g
(60) 2 (sin 30° )2
Ymaks = _______________________
2(10)
(60) 2 (1/2 )2
Ymaks = _______________________ = 45 meter
20
Soal No. 5
Peluru ditembakkan condong ke atas dengan kecepatan awal v = 1,4 x 103 m/s dan mengenai sasaran yang jarak mendatarnya sejauh 2 x 105 m. Bila percepatan gravitasi 9,8 m/s2, maka elevasinya adalah n derajad, dengan n sebesar….
A. 10
B. 30
C. 45
D. 60
E. 75
(Sumber soal UMPTN 1993)
Pembahasan
Data dari soal:
vo = 1,4 x 103 m/s
Xmaks = 2 x 105 m
α = …….
Dari rumus jarak mendatar maksimum:
vo 2 sin 2 α
Xmaks = _______________________
g
(1,4 x 103) 2 sin 2 α
2 x 105 = ______________________________
9,8
2 x 105 x 9,8
sin 2 α = ______________________________
(1,4 x 103) 2
sin 2 α = 1
sin 2α = sin 90°
α = 90°/2 = 45 °
Update 12 Maret 2017
Kumpulan Soal Ujian
1) Sebuah pesawat tempur bergerak dengan kelajuan tetap 100 m/s pada ketinggian 600 kaki dari atas tanah.
Beberapa saat kemudian pesawat itu menembakkan rudal dengan arah lurus ke belakang. Rudal bergerak dengan kecepatan awal 75 m/s.
Dengan anggapan bahwa kecepatan pesawat dijaga tetap konstan setelah menembakkan rudal maka jarak mendatar tempat jatuhnya rudal dengan posisi pesawat saat rudal menyentuh tanah adalah….(gunakan g = 10 m/s2 , 1 kaki = 0,3 m)
A. 450 m
B. 600 m
C. 1.050 m
D. 1.200 m
E. 1.450 m
2) Komponen-komponen kecepatan suatu benda yang bergerak mengikuti gerak peluru adalah….
A. besar komponen pada arah mendatar selalu tetap, pada arah vertikal berubah-ubah
B. besar komponen pada arah mendatar berubah-ubah pada arah vertikal tetap
C. besar komponen pada arah mendatar dan arah vertikal tetap
D. besar komponen pada arah mendatar dan arah vertikal berubah
E. besar komponen pada arah mendatar dan arah vertikal tetap pada setengah lintasan pertama dan berubah pada setengah lintasan berikutnya
3) Sebuah batu dilempar hingga menempuh lintasan parabolic. Jika batu berada di udara selama 4 sekon dan percepatan gravitasi bumi di tempat tersebut 10 m/s2, maka ketinggian maksimum yang dicapai batu adalah….
A. 48 m
B. 30 m
C. 30 m
D. 20 m
E. 12 m
4) Dua buah peluru ditembakkan dengan kecepatan awal yang sama dari dari sebuah pistol dengan sudut peluncuran 30° dan 60°. Perbandingan tinggi maksimum yang dicapai peluru pertama dan peluru kedua adalah….
A. 1 : 2
B. 1 : 3
C. 2 : 1
D. 1 : √3
E. √3 : 1
5) Dua buah peluru ditembakkan dengan kecepatan awal yang sama dari dari sebuah pistol dengan sudut peluncuran 37° dan 53°. Perbandingan jarak mendatar maksimum yang dicapai peluru pertama dan peluru kedua adalah….
A. 1 : 1
B. 1 : 2
C. 2 : 1
D. 2 : 3
E. 3 : 2
6) Sebuah peluru ditembakkan dengan kecepatan awal 60 m/s dan dengan sudut elevasi 30°. Tinggi maksimum yang dicapai peluru adalah….
A. 30 m
B. 45 m
C. 50 m
D. 90 m
E. 100 m
7) Peluru ditembakkan condong ke atas dengan kecepatan awal ν = 1,4 x 103 m/s dan mengenai sasaran yang jarak mendatarnya sejauh 2 x 105 m. Bila percepatan gravitasi 9,8 m/s2, maka sudut elevasi penembakan peluru adalah….
A. 10°
B. 30°
C. 45°
D. 60°
E. 75°
8) Sebuah peluru ditembakkan dengan sudut elevasi 37° dan kecepatan awal 100 m/s. Jika percepatan gravitasi bumi di tempat tersebut adalah 10 m/s2, maka kecepatan peluru saat mencapai ketinggian maksimum adalah….(tan 37° = 0,75)
A. 0 m/s
B. 20 m/s
C. 40 m/s
D. 60 m/s
E. 80 m/s
9) Sebuah peluru ditembakkan dengan sudut elevasi 37° dan kecepatan awal 100 m/s. Jika percepatan gravitasi bumi di tempat tersebut adalah 10 m/s2, maka besar komponen kecepatan peluru pada arah vertikal saat t = 1 sekon adalah….(tan 37° = 0,75)
A. 20 m/s
B. 30 m/s
C. 40 m/s
D. 50 m/s
E. 60 m/s
10) Sebuah roket ditembakkan dengan kecepatan awal 1500 m/s dengan sudut luncur 45° terhadap tanah. Waktu yang diperlukan roket untuk mencapai jarak mendatar maksimum adalah….(g = 10 m/s2)
A. 100√2 s
B. 200√2 s
C. 300√2 s
D. 400√2 s
E. 500√2 s
11) Sebuah pesawat terbang bergerak mendatar dengan kecepatan 200 m/s melepaskan bom dari ketinggian 500 m.
Jika bom jatuh di B dan g = 10 m/s2, maka jarak AB adalah….
A. 500 m
B. 1.000 m
C. 1.500 m
D. 1.750 m
E. 2.000 m
12) Sebuah mobil hendak menyeberangi sebuah parit yang lebarnya 4,0 meter. Perbedaan tinggi kedua sisi parit adalah 15 cm, seperti yang ditunjukkan gambar di bawah ini.
Jika percepatan gravitasi g = 10 m/s2, maka besar kelajuan minimum agar penyeberangan mobil itu tepat dapat berlangsung adalah….
A. 10 m/s
B. 15 m/s
C. 17 m/s
D. 20 m/s
E. 23 m/s