Menu Close

Kedudukan Dua Garis berserta conto soal

afdhalilahi08 0 Comments
Pernahkah kalian mengikuti lomba baris-berbaris untuk kegiatan 17 Agustus? Atau hanya sekadar menonton pasukan baris-berbaris? Jika diperhatikan, kegiatan baris-berbaris terdiri atas 3 atau 4 banjar ke belakang. 
 
Salah satu penilaiannya adalah kerapian dalam menyusun barisan. Tiap banjar harus mempertahankan banjarnya agar selalu membentuk garis lurus dan jaraknya selalu konstan antar banjar. Pada kasus ini, kalian dapat mengamati bahwa kedua banjar barisan tersebut tidak pernah berpotongan, selalu sejajar dengan jarak yang sama. Kedua banjar barisan tersebut bisa kita misalkan dua buah garis lurus, sehingga keduanya tidak saling berpotongan dan disebut garis sejajar. 

Permasalahan tersebut merupakan salah satu contoh dari kedudukan dua garis. Apakah kedudukan garis hanya sejajar? Untuk tahu jawabannya, yuk simak topik ini dengan seksama. 

Sebelum kalian belajar tentang kedudukan dua garis, kalian perlu memahami terlebih dahulu pengertian sebuah garis. Untuk itu, mari kita simak penjelasan berikut ini.

Garis 

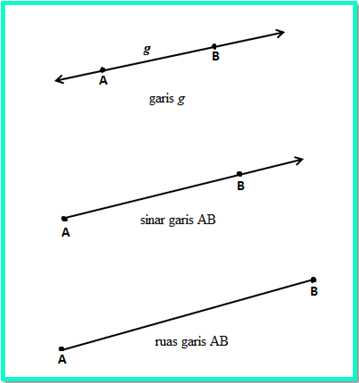
Suatu garis terbentuk dari hubungan antara dua titik yang tidak berhimpit dan membentuk garis lurus. Suatu garis tidak memiliki ujung atau pangkal. Jika suatu garis memiliki pangkal tapi tidak berujung, dinamakan sinar garis, sedangkan jika suatu garis memiliki pangkal dan ujung, dinamakan ruas garis. Penamaan suatu garis dapat dituliskan menggunakan huruf kecil seperti g, h, k, l dan sebagainya, sedangkan penamaan untuk ruas garis dapat dituliskan nama titik penyusunya.

Perhatikan gambar berikut ini.
Kalian tentu telah paham tentang pengertian garis. Sekarang, mari kita belajar tentang kedudukan dua garis. 

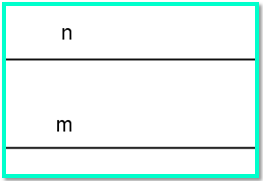
Misalkan diberikan dua buah garis yaitu m dan n. Sifat-sifat kedudukan dua garis tersebut yaitu sebagai berikut.

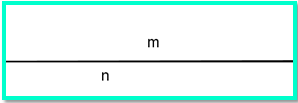
Dua Garis Sejajar


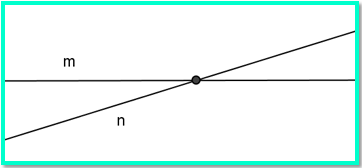
Garis m dan n dikatakan sejajar jika kedua garis itu tidak pernah berpotongan di titik manapun meskipun diperpanjang sampai tak berhingga. Dua garis yang sejajar dinotasikan dengan ” // ” dan selalu dapat ditempatkan pada bidang yang sama.
Dua Garis Berpotongan 

Garis m dan n dikatakan saling berpotongan apabila garis tersebut terletak pada satu bidang datar dan mempunyai satu titik potong atau titik persekutuan.
 
 
Dua Garis Berimpit 

Garis m dan n dikatakan saling berimpit apabila garis tersebut terletak pada satu garis lurus pada suatu bidang. Syarat minimal dua garis berimpit adalah dua titik pada masing-masing garis saling berimpit.
 
Dua Garis Bersilangan 

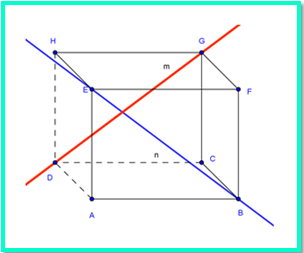
Garis m dan n dikatakan bersilangan apabila garis-garis tersebut tidak terletak pada satu bidang datar dan tidak akan berpotongan apabila diperpanjang.
 
 
Garis m terletak pada bidang DCGH dan garis n terletak pada bidang ABFE. Garis m dan garisn saling bersilangan. 

Materi tersebut cukup membuat kalian paham bukan? Untuk menambah pemahaman kalian, perhatikan contoh berikut ini.

contoh soal 

Contoh 1:
Diketahui kubus ABCD.EFGH. Kemungkinan kedudukan garis-garis diagonal bidang pada masing masing sisi kubus adalah ….
Penyelesaian:
Perhatikan gambar kubus ABCD.EFGH berikut ini.

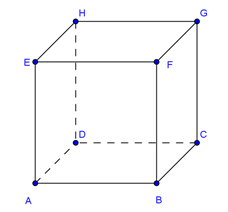
Misalkan diambil salah satu diagonal bidang yaitu AC.
Diagonal bidang AC akan berpotongan dengan diagonal bidang BD pada bidang ABCD.
Diagonal bidang AC akan sejajar dengan diagonal bidang EG pada bidang ACGE.
Diagonal bidang AC akan bersilangan dengan diagonal bidang FH pada bidang EFGH.
Dengan demikian, untuk setiap diagonal bidang pada kubus selalu bisa ditemukan garis lain yang sejajar, berpotongan dan bersilangan.

Contoh 2:
Diberikan garis k, l, m. Jika garis k sejajar dengan garis m dan garis m sejajar dengan garis l, maka kemungkinan kedudukan garis k dan l adalah ….
Penyelesaian:
Ada 2 kemungkinan, yaitu:
Pada kasus 1, garis k akan sejajar dengan garis l.
Pada kasus 2, garis k akan berimpit dengan garis l.
Garis k dan l tidak akan berpotongan dan bersilangan.
Contoh 3:
Perhatikan bangun layang-layang berikut ini.
Jika ruas garis TV dan RS diperpanjang, maka kedudukan kedua garis adalah ….
Penyelesaian:
Perhatikan bahwa RSTV merupakan bangun layang-layang sehingga ruas garis TV dan RStidak sejajar.
Dengan demikian, jika ruas garis TV dan RS diperpanjang maka kedua garis akan berpotongan di suatu titik.
 sumber :
 
Post Views: 15

Leave a Reply