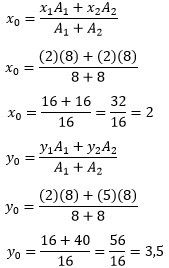Kumpulan Soal Titik Berat Benda Lengkap dengan Pembahasannya
Berikut ini beberapa contoh soal mengenai titik berat gabungan dari benda-benda yang mempunyai panjang, luasan maupun volume.
Contoh 1
Tentukan koordinat titik berat dari bangun berikut!
Pembahasan:
Bangun diatas adalah benda berdimensi satu. Benda itu dibagi atas 4 bagian seperti pada gambar berikut.
Masing-masing kurva membentuk garis lurus.
Kurva I (titik berat di z1)
Panjang : l1 = 4
x1 = 2
y1 = 5
Kurva II (titik berat di z2)
Panjang : l2 = 6
x2 = 3
y2 = 3
Kurva III (titik berat di z3)
Panjang : l3 = 6
x3 = 6
y3 = 3
Kurva IV (titik berat di z4)
Panjang : l4 = 4
x4 = 6
y4 = 6
Titik berat benda ditentukan oleh persamaan berikut:
Jadi koordinat titik berat bangun diatas adalah z0 (4,3 ; 4)
Contoh 2
Tentukan koordinat titik berat potongan karton homogen pada gambar berikut!
Pembahasan:
Gambar diatas dapat kita bagi menjadi 2 bagian, yaitu persegi panjang I (warna kuning) dan persegi panjang II (warna hijau). Ingat titik berat persegi panjang terletak pada perpotongan diagonal-diagonalnya!
Persegi panjang I:
x1 = 0,5
y1 = 2,5
A1 = 1 × 5 = 5
Persegi panjang II:
x2 = 1 + 2 = 3
y2 = 0,5
A2 = 1 × 4 = 4
Sehingga:
Contoh 3
Tentukan letak koordinat titik berat dari bidang yang diarsir pada gambar berikut!
Pembahasan:
Bidang dibagi atas 2 bagian, yaitu persegi panjang yang dianggap utuh tidak berlubang dan lubang berbentuk segitiga (bidang yang tidak diarsir).
Bidang I (Persegi panjang)
A1 = 8 x 6 = 48
x1 = 3
y1 = 4
Bidang II (segitiga)
A2 = ½ (8 x 3) = 12
x2 = 6 – (⅓ × tinggi segitiga) = 6 – (3/3) = 5
y2 = 4
Sehingga:
Dengan demikian koordinat titik berat bidang yang diarsir adalah (7/3 , 4)
Contoh 4
Tentukan koordinat titik berat dari bangun berikut terhadap sumbu x!
Pembahasan:
Diukur terhadap sumbu x artinya yang dicari adalah yo
Bangun I (persegi panjang)
A1 = 3 × 6 = 18
y1 = 1,5
Bangun I (segitiga)
A2 = ½ (3 × 3) = 4,5
y2 = 3 + (⅓ × tinggi segitiga) = 3 + 1 = 4
Sehingga
Contoh 5
Tentukan letak titik berat benda berbentuk huruf T seperti pada gambar berikut!
Pembahasan:
Bidang I (Persegi panjang bawah)
A1 = 2 × 4 = 8 cm²
x1 = 2 cm
y1 = 2 cm
Bidang II (Persegi panjang atas)
A2 = 2 × 4 = 8 cm²
x2 = 2 cm
y2 = 4 + 1 = 5 cm
Sehingga:
Jadi koordinat titik berat bangun diatas adalah (2 ; 3,5)
Contoh 6
Pada gambar dibawah ini sebuah benda terdiri dari tabung pejal dan kerucut. Tentukan titik berat benda bervolume tersebut dari alasnya!
Pembahasan:
Bangun I (tabung pejal)
V1 = π r² t = π 3² (10) = 90 π
y1 = 5
Bangun I (kerucut)
V2 = ⅓ π r² t = ⅓ π 3² (12) = 36 π
y2 = 10 + (¼ × tinggi kerucut) = 10 + 3 = 13
Sehingga:
Contoh 7
Pada gambar dibawah ini sebuah benda terdiri dari tabung pejal dan setengah bola pejal. Tentukan titik berat benda bervolume tersebut dari alasnya!
Pembahasan:
Bangun I (tabung pejal)
V1 = π r² t = π 4² (10) = 160 π
y1 = 5
Bangun I (setengah bola pejal)
V2 = ½ volume bola = ½ (4/3 π R³) = ½ (4/3 π (4)³) = 42,7 π
y2 = 10 + (3/8 R) = 10 + (3/8 (4)) = 10 + 1,5 = 11,5
Sehingga:
Sumber:
Go to Original Article