SIFAT – SIFAT LOGARITMA, CONTOH SOAL DAN PENYELESAIANNYA
18 DESEMBER 2015 BY NURLAELA EKA CAHYATI
A. Definisi Logaritma
Logaritma adalah operasi matematika yang merupakan invers (kebalikan) dari eksponen atau pemangkatan.
Atau dengan pengertian lain, bentuk eksponen bila dinyatakan dengan notasi logaritma adalah
bila dinyatakan dengan notasi logaritma adalah  .
.
dengan :
a = basis atau bilangan pokok
b = hasil atau range logaritma
c = numerus atau domain logaritma.
Sebagai catatan, bahwa penulisan sama artinya dengan
sama artinya dengan  .
.
Atau dengan pengertian lain, bentuk eksponen
 bila dinyatakan dengan notasi logaritma adalah
bila dinyatakan dengan notasi logaritma adalah  .
.dengan :
a = basis atau bilangan pokok
b = hasil atau range logaritma
c = numerus atau domain logaritma.
Sebagai catatan, bahwa penulisan
 sama artinya dengan
sama artinya dengan  .
.
B. Sifat – sifat Logaritma
Jika a>0, a ≠ 1, m ≠ 1, b>0 dan c>0, maka berlaku :
Jika a>0, a ≠ 1, m ≠ 1, b>0 dan c>0, maka berlaku :

Contoh Soal :
1. Diketahui dan
dan 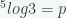 . Nilai
. Nilai  dinyatakan dalam p dan q adalah … (UN SMA 2013)
dinyatakan dalam p dan q adalah … (UN SMA 2013)
1. Diketahui
Penyelesaian :

2. Hasil dari  adalah … (UN SMA 2012)
adalah … (UN SMA 2012)
 adalah … (UN SMA 2012)
adalah … (UN SMA 2012)
Penyelesaian :

3. 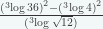 = … (Sipenmaru 1987)
= … (Sipenmaru 1987)
Penyelesaian :
Ingat sifat aljabar


Maka gunakan sifat tersebut untuk menyelesaikan pembilangnya.
Jadi,

Jadi,

4.  sama dengan … (SPMB 2012)
sama dengan … (SPMB 2012)
Penyelesaian :

5. 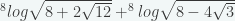 sama dengan …
sama dengan …
Penyelesaian :
Ingat bahwa :


Maka persamaan dapat disederhanakan menjadi :


6. Jika  , maka
, maka 
sama dengan … (UMPTN 2005)
sama dengan … (UMPTN 2005)
Penyelesaian :


Cara Cepat :
Bentuk  akan terdefinisi jika
akan terdefinisi jika  . Maka substitusikan sembarang x anggota ℝ kecuali
. Maka substitusikan sembarang x anggota ℝ kecuali 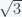 .
.
 akan terdefinisi jika
akan terdefinisi jika  . Maka substitusikan sembarang x anggota ℝ kecuali
. Maka substitusikan sembarang x anggota ℝ kecuali
Misal x = 3, maka f(3) + f(1) = -1 + 0 = -1.
7. Jika  , maka
, maka 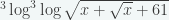 = …
= …
Penyelesaian :


Maka,


8. Jika x memenuhi persamaan  , maka
, maka  = …
= …
Penyelesaian :

Jadi,


9. Nilai x yang memenuhi  adalah … (UMPTN 2000)
adalah … (UMPTN 2000)
Penyelesaian :

10. Jika 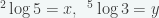 , maka nilai
, maka nilai 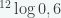 dalam x dan y adalah …
dalam x dan y adalah …
Penyelesaian :

11. Jika 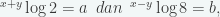 dengan x>y>0 maka
dengan x>y>0 maka 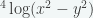 = … (UM UGM 2010)
= … (UM UGM 2010)
Penyelesaian :

Dari persamaan (1) dan (2) di dapat :
12. What is the value of the expression
Penyelesaian :
Ingat bahwa  adalah bentuk lain dari
adalah bentuk lain dari 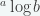 dan
dan 
Note : 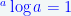
Jadi,
sumbercahaya etika