Pada pembahasan ini kita akan berlatih untuk membuktikan suatu pernyataan matematis dengan menggunakan induksi matematika. Metode pembuktian ini digunakan untuk membuktikan pernyataan yang bergantung pada bilangan bulat positif.

Prinsip Induksi Matematika
Untuk setiap bilangan bulat positif n, misalkan P(n) adalah pernyataan yang bergantung pada n. Jika
P(1) benar, dan
untuk setiap bilangan bulat positif k, jika P(k) benar maka P(k + 1) benar
maka pernyataan P(n) bernilai benar untuk semua bilangan bulat positif n.
Untuk menerapkan prinsip ini, kita harus melakukan dua langkah:
Langkah 1 Buktikan bahwa P(1) benar. (langkah dasar)
Langkah 2 Anggap bahwa P(k) benar, dan gunakan anggapan ini untuk membuktikan bahwa P(k + 1) benar. (langkah induksi)
Perlu diingat bahwa dalam Langkah 2 kita tidak membuktikan bahwa P(k) benar. Kita hanya menunjukkan bahwa jika P(k) benar, maka P(k + 1) juga bernilai benar. Anggapan bahwa pernyataan P(k) benar disebut sebagai hipotesis induksi.
Untuk menerapkan Prinsip Induksi Matematika, kita harus bisa menyatakan pernyataan P(k + 1) ke dalam pernyataan P(k) yang diberikan. Untuk menyatakan P(k + 1), substitusi kuantitas k + 1 ke k dalam pernyataan P(k).
Soal 1: Pendahuluan
Tentukan pernyataan P(k + 1) untuk masing-masing pernyataan P(k) berikut.
P(k): Sk = [k²(k + 1)²]/4
P(k): Sk = 1 + 5 + 9 + … + [4(k – 1) – 3] + (4k – 3)
P(k): k + 3 < 5k²
P(k): 3k ≥ 2k + 1
Pembahasan
Kita substitusi k + 1 ke k dalam pernyataan P(k).
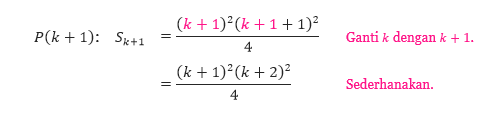
Untuk mendapatkan pernyataan P(k + 1), kita ganti k pada pernyataan P(k) dengan k + 1.
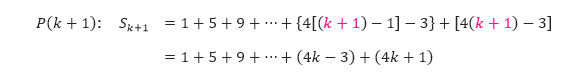
Kita substitusi k dengan k + 1, dan kita peroleh
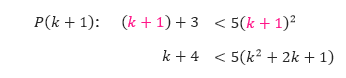
Serupa dengan soal-soal sebelumnya, kita substitusi k pada pernyataan P(k) dengan k+ 1 untuk mendapatkan pernyataan P(k + 1).
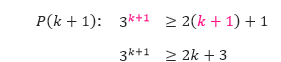
Ketika menggunakan induksi matematika untuk membuktikan rumus penjumlahan (seperti pada Soal 2), akan sangat membantu jika kita berpikir bahwa Sk + 1 = Sk + ak + 1, di mana ak + 1 adalah suku ke-(k + 1) dari penjumlahan tersebut.
Soal 2: Menggunakan Induksi Matematika
Gunakan induksi matematika untuk membuktikan rumus
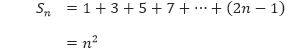
untuk semua bilangan bulat n ≥ 1.
Pembahasan Induksi matematika terdiri dari dua bagian yang berbeda.
Pertama, kita harus menunjukkan bahwa rumus tersebut benar ketika n = 1. Ketika n = 1, rumus tersebut benar, karena
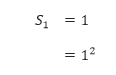
Bagian kedua induksi matematika memiliki dua langkah. Langkah pertama adalah menganggap bahwa rumus tersebut benar untuk sebarang bilangan bulat k. Langkah kedua adalah menggunakan anggapan ini untuk membuktikan bahwa rumus tersebut benar untuk bilangan bulat selanjutnya, k + 1. Anggap bahwa rumus
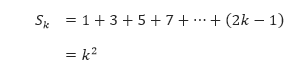
bernilai benar, kita harus menunjukkan bahwa rumus Sk + 1 = (k + 1)² benar.
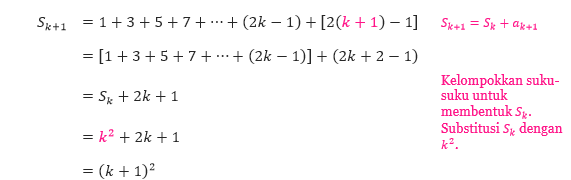
Dengan menggabungkan hasil pada langkah (1) dan (2), kita dapat menyimpulkan dengan induksi matematika bahwa rumus tersebut benar untuk semua bilangan bulat n ≥ 1.
sumber:https://yos3prens.wordpress.com/2015/10/24/25-soal-dan-pembahasan-induksi-matematika/